Back to Measure Theory Page

On this page:

• Introduction
• Set Terminology
• Ordered Sets
• Cardinality

Introduction

This is meant to consist of my notes from chapter 0 of Folland’s book.

Set Terminology

Like Folland, we will adopt the following notation:

[definition] [deftitle]Definition %counter%[/deftitle]

[/definition]

[definition] [deftitle]Definition %counter%[/deftitle]

The family of subsets (i.e. power set) of a given set $X$ is denoted

Here, $E\subseteq X$ includes the possibility that $E = X$. I may also denote $\mathcal{P}(X)$ by $2^X$. [/definition]

[definition] [deftitle]Definition %counter%[/deftitle]

We say that an indexed family of sets $\{E_\alpha\}$ is disjoint provided that the $E_\alpha$’s are all pairwise disjoint. [/definition]

[definition] [deftitle]Definition %counter%[/deftitle]

The limit superior of the indexed family of sets $\{E_n\}$ is the set

and the limit inferior is defined as

[/definition]

[theorem] [thmtitle]Proposition %counter%[/thmtitle]

[/theorem]

[proof] Let $x \in \limsup E_n$. Then we see that $x \in \bigcup_{n=k}^\infty E_n$ for every $k \ge 1$. If $x$ were in finitely many $E_n$, there is some largest $N$ for which $x \in E_N$ and $x \notin E_{N+m}$ for any $m \ge 1$. But then this would imply that $x \notin \bigcup_{n=N+1}^\infty E_n$, contradiction. Conversely, if $x\in E_n$ for infinitely many $n$, then $x \in \bigcup_{n=k} E_n$ for every $k \ge 1$ as if there was a counterexample, then there are finitely many $E_n$ that contain $x$, contradiction. So $x \in \limsup E_n$ as desired.

Let $x \in \liminf E_n$. Then there is some $k$ for which $x \in \bigcap_{n=k}^\infty E_n$. So then $x\in E_n$ for every $n \ge k$. Thus, $x \in E_n$ for all but finitely many $n$. For the converse, if $x\in E_n$ for all but finitely many $n$, then $x\in E_n$ for $n \ge k$ where $k$ is some positive integer. Thus, $x\in \liminf E_n$ as desired. [/proof]

[definition] [deftitle]Definition %counter%[/deftitle]

Let $\set{X_\alpha}_{\alpha\in A}$ be an indexed family of sets. We define the Cartesian product $X = \prod_{\alpha \in A} X_\alpha$ of this family of sets to be

We define the $\alpha$th projection or coordinate map to be the mapping

Frequently, we will refer to the elements of $X$ as $x$ and $x_\alpha$ in place of $f$ and $f(\alpha)$. [/definition]

Ordered Sets

[definition] [deftitle]Definition %counter%[/deftitle]

Let $(X, \le)$ be a poset. We say that $\le$ is a linear or total ordering of $X$ if $x \le y$ or $y\le x$ for every $x, y \in X$. [/definition]

[definition] [deftitle]Definition %counter%[/deftitle]

Let $(X, \le)$ be a poset.

• A maximal (resp. minimal) element of $X$ is an element $x\in X$ such that $x \le y$ (resp. $x \ge y$) in $X$ implies that $y = x$.
• If $E \subset X$, then an upper (resp. lower) bound for $E$ is an element $x \in X$ such that $y \le x$ (resp. $y \ge x$) for every $y\in E$.
• If $X$ is totally orddered by $\le$, and every nonempty subset of $X$ has a unique minimal element, $X$ is said to be well ordered by $\le$. [/definition]

[theorem] [thmtitle]Zorn’s Lemma %counter%[/thmtitle]

Let $X$ be poset such that every chain of elements of $X$ has an upper bound. Then $X$ has a maximal element. [/theorem]

[theorem] [thmtitle]Theorem %counter% (Well Ordering Principle)[/thmtitle]

Every nonempty set $X$ can be well ordered. [/theorem]

[proof] Let $\mathcal{F}$ be the collection of well orderings of subsets of $X$. Given $(A, \le_1), (B, \le_2) \in \mathcal{F}$, we say that $(A, \le_1) \le (B, \le_2)$ if and only if

1. $A \subset B$ and $\le_2$ extends $\le_1$. That is, $x \le_1 y$ implies $x \le_2 y$ for every $x, y \in A$.
2. For every $x\in B\setminus A$, we have $y \le_2 x$ for every $y\in A$.

Clearly $\mathcal{F}$ is nonempty as any singleton is trivially well ordered and $X$ is nonempty. Now suppose that $\set{A_\alpha, \le_\alpha}$ is a chain in $\mathcal{F}$. We claim that $A = \bigcup_{\alpha} A_\alpha$ is an upper bound. It’s obvious that $A_\alpha \subseteq A$ for any $\alpha$. The induced order on $A$ is obvious and so the claim follows. By Zorn, $\mathcal{F}$ has a maximal element $(M, \le)$. It is clear that $M = X$ since if it was not, $M \cup \set{a}$, where $a \in X \setminus M$ would strictly contain $M$ and clearly $M \cup \set{a} \in \mathcal{F}$, violating maximality. [/proof]

[theorem] [thmtitle]Theorem %counter% (Axiom of Choice)[/thmtitle]

If $\set{X_\alpha}$ is a nonempty collection of nonempty sets, then $\prod_{\alpha} X_\alpha$ is nonempty. [/theorem]

[proof] Let $X = \bigcup_{\alpha} X_\alpha$. By the Well-Ordering Principle, we can well order $X$. Thus, define $f(\alpha)$ to be the minimal element of $X_\alpha$. By $f\in X$ and so $X$ is nonempty as desired. [/proof]

There is a result that is much more commonly referred to as the Axiom of Choice.

[theorem] [thmtitle]Corollary %counter% (Axiom of Choice)[/thmtitle]

If $\set{X_\alpha}$ is a disjoint collection of nonempty sets, there is a set $Y \subset X \coloneqq \bigcup_\alpha X_\alpha$ such that $Y \cap X_\alpha$ contains precisely one element for each $\alpha \in A$. [/theorem]

[proof] By the Axiom of Choice, we know that $X$ is nonempty so there is some $f\in X$. We claim that if $Y \coloneqq f(A)$, then $Y$ satisfies the desired claim. Indeed, given $f(\alpha) \in f(A)$, we know taht $f(\alpha) \in X_\alpha$ so $Y \cap X_\alpha$ is nonempty. Now, if there is any other element $\beta$ in $Y \cap X_\alpha$, then $f(\beta) \in X_\beta$ so $\beta\in X_\alpha \cap X_\beta$, contradicting the disjointness of the $X_\alpha$’s. Thus, $Y \cap X_\alpha = \set{f(\alpha)}$. [/proof]

Cardinality

[definition] [deftitle]Definition %counter%[/deftitle]

Let $X$ and $Y$ be nonempty sets.

• We say $\card(X) \le \card(Y)$ to mean that there is some injective $X \injto Y$.
• We say $\card(X) = \card(Y)$ to mean there is a bijection $X \to Y$.
• We say $\card(X) \ge \card(Y)$ to mean there is a surjection $X \surjto Y$. [/definition]

In general, we will avoid working with empty sets to avoid special arguments for $\emptyset$.

[theorem] [thmtitle]Proposition %counter%[/thmtitle]

[/theorem]

[proof] ($\implies$) Let $f:X \injto Y$ be an injection. We define a function $g:Y \to X$ by defining $g(y) = f^{-1}(y)$. As $f$ is an injection, $g(y)$ is a singleton which we identity with its lone element.

($\impliedby$) Let $g:Y \surjto X$ be a surjection. Notice that the sets $g^{-1}(x)$ are nonempty (by surjectivity) and disjoint (also by surjectivity). Thus, by the axiom of choice, there exists some $f \in \prod_{x\in X} g^{-1}(x)$. Any such $f$ is an injection. Indeed, suppose

Now $f(x_1) \in g^{-1}(x_1)$ and $f(x_1) \in g^{-1}(x_2)$. But since $g^{-1}(x_1)$ and $g^{-1}(x_2)$ are disjoint if and only if $x_1 \neq x_2$, it follows that $x_1 = x_2$ (otherwise we would contradict $f(x_1) = f(x_2)$). [/proof]

[theorem] [thmtitle]Proposition %counter%[/thmtitle]

For any sets $X$ and $Y$, either $\card(X) \le \card(Y)$ or $\card(Y) \le \card(X)$.

[/theorem]

[proof] Let $\mathcal{F}$ consist of all injections from subsets of $X$ to $Y$. We impose a partial ordering upon $\mathcal{F}$ by setting $f:A \to B \le g:C \to D$ if and only if $g$ extends $f$. Clearly, $\mathcal{F}$ is nonempty as we may define

where $x \in X$ and $y\in Y$ are chosen arbitrarily. Now if we have a chain $\{f_\alpha:A_\alpha \to B_\alpha\}$ in $\mathcal{F}$, then we define

by setting $f(a) = f_\alpha(a)$ where $f_\alpha$ is chosen to be the minimal element of the chain for which $a$ is defined. Now if $f(a_1) = f(a_2)$, then there is some $A_\alpha$ which contains both $a_1$ and $a_2$. Furthermore,

Thus, $f$ is injective. So every chain has an upper bound and Zorn’s Lemma implies that $\mathcal{F}$ has a maximal element $f:A \to B$. Suppose that $A \neq X$ and $B \neq Y$. Then we can define an extension $F$ of $f$ by

where $x_0 \in X \setminus A$ and $y_0 \in Y \setminus B$. This contradicts the maximality of $f$ so either $A = X$ (in which case $f$ is an injection) or $B = Y$. In the latter case, $f^{-1}$ is well-defined and is an injection $Y \to X$. [/proof]

A fairly intuitive but not easy-to-show result is that if there is an injection $X \injto Y$ and an injection $Y \injto X$, then $X$ and $Y$ are actually in bijection. Folland does not give a particularly helpful proof, in my opinion, so I replaced it with the approach that Charles Pugh takes in his Real Mathematical Analysis book.

[theorem] [thmtitle]Theorem %counter% (The Schröder-Bernstein Theorem)[/thmtitle]

If $\card(X) \le \card(Y)$ and $\card(Y) \le \card(X)$, then $\card(X) = \card(Y)$. [/theorem]

[proof] By definition, there $f:X \to Y$ and $g:Y \to X$ be injections. Our goal will be to construct a bijection $h:X \to Y$. Consider the following diagram:

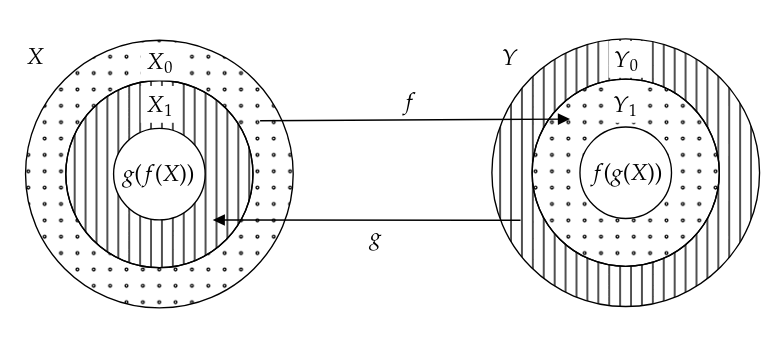
In $X$, we define $X_0 \subseteq X$ to consist of the $x \in X$ which are NOT in the range of $g$. We define $X_1 \subseteq X$ to consist of the $x \in X$ which ARE in the range of $g$ but not in $g(f(X))$. We define $Y_0$ and $Y_1$ in a similar way.

We begin defining $h$ as follows. Pick $x \in X$.

• In the case where $x \in X_0$, we just set $h(x) = f(x)$.
• In the case where $x \in X_1$, we set $h(x) = g^{-1}(x)$.

Clearly, $h$ is a bijection on $X_0$ and $X_1$ with obvious inverses. Now, for $g(f(X))$ and $f(g(X))$, notice that we have an identical scenario where we have an injection from $A \to B$ and an injection $B\to A$, which is our original problem. So we repeat the process above to obtain $X_2$ and $X_3$, and $Y_2$ and $Y_3$, where $f$ injects $X_2$ into $Y_3$ and $g$ injects $Y_2$ into $X_3$. Continuing this process indefinitely gives rise to a bijection

where

We then define

We claim that $f$ bijects $X_\infty$ to $Y_\infty$. To see that $f$ actually sends $X_\infty$ to $Y_\infty$, we pick out some $x \in X_\infty$. Then if $f(x) \in Y_i$, then we can invert $f(x)$ via $h_0^{-1}$ which would imply that $x \in X_j$ where $i = j \pm 1$. Injectivity follows from the fact that a restriction of the codomain of an injection is still an injection. Surjectivity arises by noting that if there is some $y\in Y_\infty$ for which $x \coloneqq f^{-1}(y) \in X_i$ for some $X_i$, then $h_0$ sends $x$ to some $Y_j$. If $j$ is even, then $h_0(x) = f(x) = y$ implies $y\notin Y_\infty$ which is obviously a contradiction. If $j$ is odd, then $h_0(x) = g^{-1}(x)$ which also implies $y \notin Y_\infty$. Thus, $f$ bijects $X_\infty$ and $Y_\infty$ so we can define $h:X \to Y$ by

[/proof]

[example] [extitle]Example %counter% (Bijecting $(a, b)$ and $[a,b]$)[/extitle]

A classic example of the Schröder-Bernstein is to show that $(a, b)$ and $[a, b]$ are in bijection non-constructively. Clearly, $(a, b)$ embeds into $[a, b]$. The converse direction is a little harder: Let $g:[a, b] \to (a, b)$ be defined by

Obviously this function is increasing and $g(a) > a$ and $g(b) < b$. Intuitively, this map “takes up” the middle two-fourths of $(a, b)$. So the Schröder-Bernstein Theorem implies there must be some kind of bijection of $(a, b)$ and $[a, b]$. [/example]

[theorem] [thmtitle]Proposition %counter%[/thmtitle]

For any set $X$, $\card(X) < \card(2^X)$. [/theorem]

[proof] Clearly there is an injection $X \to 2^X$ by sending $x\mapsto \{x\}$ so $\card(X) \le \card(2^X)$. Let us now show that equality does not hold. Suppose that $g$ is any function $X \to 2^X$ and set

Our goal is to show that $g$ is NOT surjective by showing that $g$ does NOT map onto $Y$. By construction, $Y \notin g(X)$. Indeed, if there was some $y \in X$ for which $g(y) = Y$, then we can ask if $y\in Y$ or $y\notin Y$. If $y \in Y$, then $y \notin g(y) = Y$ which is a contradiction. If $y\notin Y$, then $y\in g(y) = Y$ which is also a contradiction. So $Y \notin g(X)$ and it follows that $g$ fails to be surjective as $Y \in 2^X$. [/proof]

[definition] [deftitle]Definition %counter%[/deftitle]

The set $X$ is countable or denumerable if $\card(X) \le \card(\NN)$. If $X$ is countable but not finite, then we say that $X$ is countably infinite. [/definition]

[theorem] [thmtitle]Theorem %counter%[/thmtitle]

Let $X$ and $Y$ be countable. Then so is $X \times Y$. [/theorem]

[proof] Granted that $\NN^2$ is countable, we see that $X \times Y$ is as well since this would imply

Now we show that $\NN^2$ is countable. To do this, we use the “usual diagonalization” proof where we send $n$ to the $n$th term in the list

Clearly this is a bijection. [/proof]

[theorem] [thmtitle]Theorem %counter%[/thmtitle]

Countable unions of countable sets are also countable. [/theorem]

[proof] Let $A$ be countable and $X_a$ be countable for every $a \in A$. Since each $X_a$ is countable, there is a surjective map $f_a:\NN \to X_a$ for each $a \in A$. Thus, we can define the map

Clearly this map is a surjection. Thus, $\card(\NN\times A) \ge \card(\bigcup_{a\in A} X_a)$ so the desired claim follows. [/proof]

[theorem] [thmtitle]Theorem %counter%[/thmtitle]

If $X$ is countably infinite, then $\card(X) = \card(\NN)$. As such, we denote this by saying $\card(X) = \aleph_0$. [/theorem]

[proof] As $\card(X) \le \card(\NN)$, it follows that there is an injection $X \injto \NN$. Identifying $X$ with its image in $\NN$, we will define a function $f:\NN \to X$ as follows:

• Set $f(1) = \min X$ (which exists by the well-ordering principle).
• Set $f(2) = \min(X\setminus \{f(1)\})$.
• Set $f(3) = \min(X\setminus \{f(1), f(2)\})$.
• …
• Set $f(k) = \min(X \setminus \{f(i) \in [k-1]\})$.

Clearly $f$ is an injection so we obtain $\card(\NN) \le \card(X)$. [/proof]

[theorem] [thmtitle]Theorem %counter%[/thmtitle]

$\ZZ$ and $\QQ$ are countable. [/theorem]

[proof] Recall that $\ZZ = (-\NN)\sqcup 0 \sqcup \NN$ so $\ZZ$ is necessarily countable. For $\QQ$, note that $\QQ \subseteq \ZZ^2$ which is countable. [/proof]

[definition] [deftitle]Definition %counter%[/deftitle]

A set $X$ is aid to have the cardinality of the continuum if $\card(X) = \card(\RR)$. In such a case, we will denote this by saying $\card(X) = \mathfrak{c}$. [/definition]

[theorem] [thmtitle]Theorem %counter%[/thmtitle]

[/theorem]

[proof] Our goal will be to use the Schröder-Bernstein theorem.

($2^\NN \injto \RR$) Consider the mapping

By the series comparison test and Riemann Rearrangement Theorem, we know that $\sum_{n\in A} 2^{-n} \le \sum_{n=1}^\infty 2^{-n}$ so it follows that the function above is well-defined. Through series comparison, we see that $f$ is injective.

($\RR \injto 2^\NN$) Consider the map

Given any nonzero $x\in \RR$, we know that $x$ has base-2 decimal expansion. So then let $A$ correspond to the decimal expansion of $e^x$. Then $g(e^x) = x$ which gives surjectivity of $g$. Thus, we see that

By Schröder-Bernstein theorem, there is a bijection $2^\NN$ and $\RR$ and we are done. [/proof]

[theorem] [thmtitle]Corollary %counter%[/thmtitle]

If $\card(X) \ge \mathfrak{c}$, then $X$ is uncountable. [/theorem]

[proof] If $X$ is countable, then $\card(2^X) = \mathfrak{c}$. But since $\card(X) < \card(2^X) = \mathfrak{c}$, we obtain contradiction. [/proof]

[theorem] [thmtitle]Theorem %counter%[/thmtitle]

If $\card(X) \le \mathfrak{c}$ and $\card(Y) \le \mathfrak{c}$, then $\card(X \times Y) \le \mathfrak{c}$. [/theorem]

[proof] Granted that the claim is true for $X = Y = 2^\NN$, we see that $X \times Y$ can be identified with its embedding in $2^\NN \times 2^\NN$. If $\card(2^\NN\times 2^\NN) \le \mathfrak{c}$, then so is $X \times Y$.

Let us know show that the claim is actually true for $X = Y = 2^\NN$. Consider the mappings

and

We then define

Clearly $f$ is an injection (in fact, its also a bijection!). So it follows that

as desired. [/proof]

[theorem] [thmtitle]Theorem %counter%[/thmtitle]

Let $\card(A) \le \mathfrak{c}$ and $\card(X_a) \le \mathfrak{c}$ for every $a\in A$. Then $\card(\bigcup_{a\in A} X_a)\le \mathfrak{c}$. [/theorem]

[proof] There is a surjection $f_a:2^\NN \to X_a$ for every $a\in A$. Thus, we can define the map

Clearly, this map is a surjection so we obtain

and we are done. [/proof]